Ağaç, kenarlarla birbirine bağlanmış düğümlerden oluşan doğrusal olmayan hiyerarşik bir veri yapısıdır.
Neden Ağaç Veri Yapısı?
Diziler, bağlı liste, yığın ve kuyruk gibi diğer veri yapıları, verileri sıralı olarak depolayan doğrusal veri yapılarıdır.
Doğrusal bir veri yapısında herhangi bir işlemi gerçekleştirmek için veri boyutunun artmasıyla zaman karmaşıklığı da artar. Ancak bu durum günümüz hesaplama dünyasında kabul edilebilir değildir.
Ağaç veri yapıları, doğrusal olmayan bir veri yapısı olduğu için, verilere bağlı listelere göre daha hızlı ve kolay erişim sağlar, veri eklenmesinde esneklik gösterir.
Kullanım Alanları
Dosya Sistemleri: Bilgisayarınızdaki dosyalar ve klasörler, hiyerarşik bir yapıya sahip ağaç veri yapıları ile organize edilir.
Veritabanları: Veritabanlarında, tablolar ve satırlar arasındaki ilişkileri temsil etmek için ağaçlar kullanılabilir.
Web Tarayıcıları: Web tarayıcıları, web sayfalarını hiyerarşik bir yapıya sahip ağaç veri yapıları ile gösterebilir.
Derleyiciler: Derleyiciler, program kodunu analiz etmek ve işlemek için ağaç veri yapıları kullanabilir.
Yapay Zeka: Yapay zekada, karar ağaçları ve sinir ağları gibi ağaç tabanlı algoritmalar yaygın olarak kullanılmaktadır.
Ağaç veri yapıları, sunduğu birçok avantaj sayesinde bilgisayar biliminin birçok alanında önemli bir yere sahiptir. Veri organizasyonu, erişim, temsil ve algoritma tasarımı gibi konularda oldukça faydalıdırlar.
Kapsam
Ağaç (tree) yapısı, bilgisayarda çok kullanılan soyut yapılardan birisidir. Önemi ve yaygınlığı nedeniyle, dersimizde yalnızca ikili ağaç yapıları konusunda giriş bilgilerini vereceğiz.
Temel Kavramlar
İkili ağaç yapısı ağaçta bir düğümden çıkan iki dal gibidir. Literatürde dallanma noktasına kök, ata(parent), gibi adlar verilir.
Dallara ise oğul, çocuk, sibling, yaprak gibi adlar verilir.
Biz genellikle ata ve oğul terimlerini kullanacağız. Ancak yeri geldiğinde anlamı kuvvetlendirmek için öteki adlardan da birisini kullanacağız.
Örneğin aşağıdaki ağaçta, en tepede olan 10 öğesine ağacın kökü diyeceğiz.
10
/ \
4 13
/ \ / \
3 7 11 15
Bu ağaçta {4,10,13}, {3,4,7}, {11,13,15} öğelerinden oluşan 3 düğüm (node) vardır. Her düğüm bir nesneyi gösterir. Her düğüm için ortadaki sayı ata, soldaki sol oğul, sağdaki sağ oğuldur. En tepedeki 10 öğesi 0. düzeydedir. {4,13} 1. düzeyde, {3,7,11,15} 2. düzeydedir.
Bu veri yapısını C’de aşağıdaki gibi temsil edebiliriz:
struct TreeNode {int item;// düğümdeki veri TreeNode *L;// sol alt ağacı gösteren işaretçi(pointer) TreeNode *R;// sağ alt ağacı gösteren işaretçi(pointer)}
İkili ağaç yapısında her düğümün iki tane işaretçisi (pointer) vardır. Birisi (L) sol yana ayrılan dalı, ötekisi sağ (R) yana ayrılan dalı gösterir.
Sol ve sağ dallardan birisi ya da her ikisi de NULL gösterebilir. NULL gösteren dal yok demektir. İkili ağacı bir ağacın gövdesinden çıkan dallara ve yapraklara benzetebiliriz.
Yaprak: Oğulu olmayan düğüme yaprak denir.
Kenar: Ağaç yapısındaki her öğeyi atasına bağlayan yukarıya doğru yönlenmiş çizgiye kenar denilir. Her kenar, ait olduğu öğeyi atasına bağlar. Bazı ataların hem sağ hem sol oğulları vardır. Bazılarının ise ya sağ ya sol olmak üzere birer tane oğulu vardır. Bazılarının da hiç oğulu yoktur ki onlar ağaç yapısında birer yapraktır.
Derinlik: Bir öğenin (ata, düğüm) derinliği, o öğeden başlayıp köke kadar giden kenar sayısıdır.
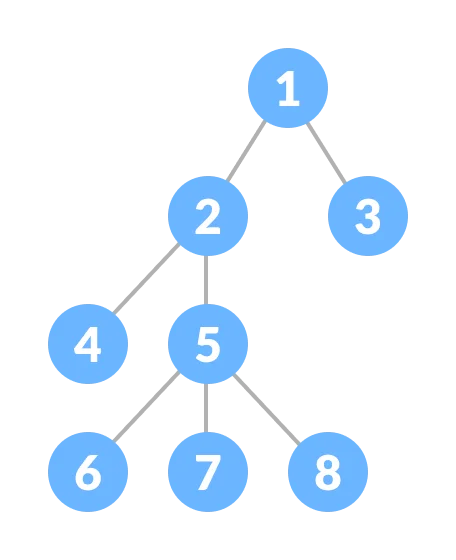
Yandaki ağaç için:
2’nin deriniliği 2’dir.
1’in derinliği 0’dır.
11’in derinliği 3’tür.
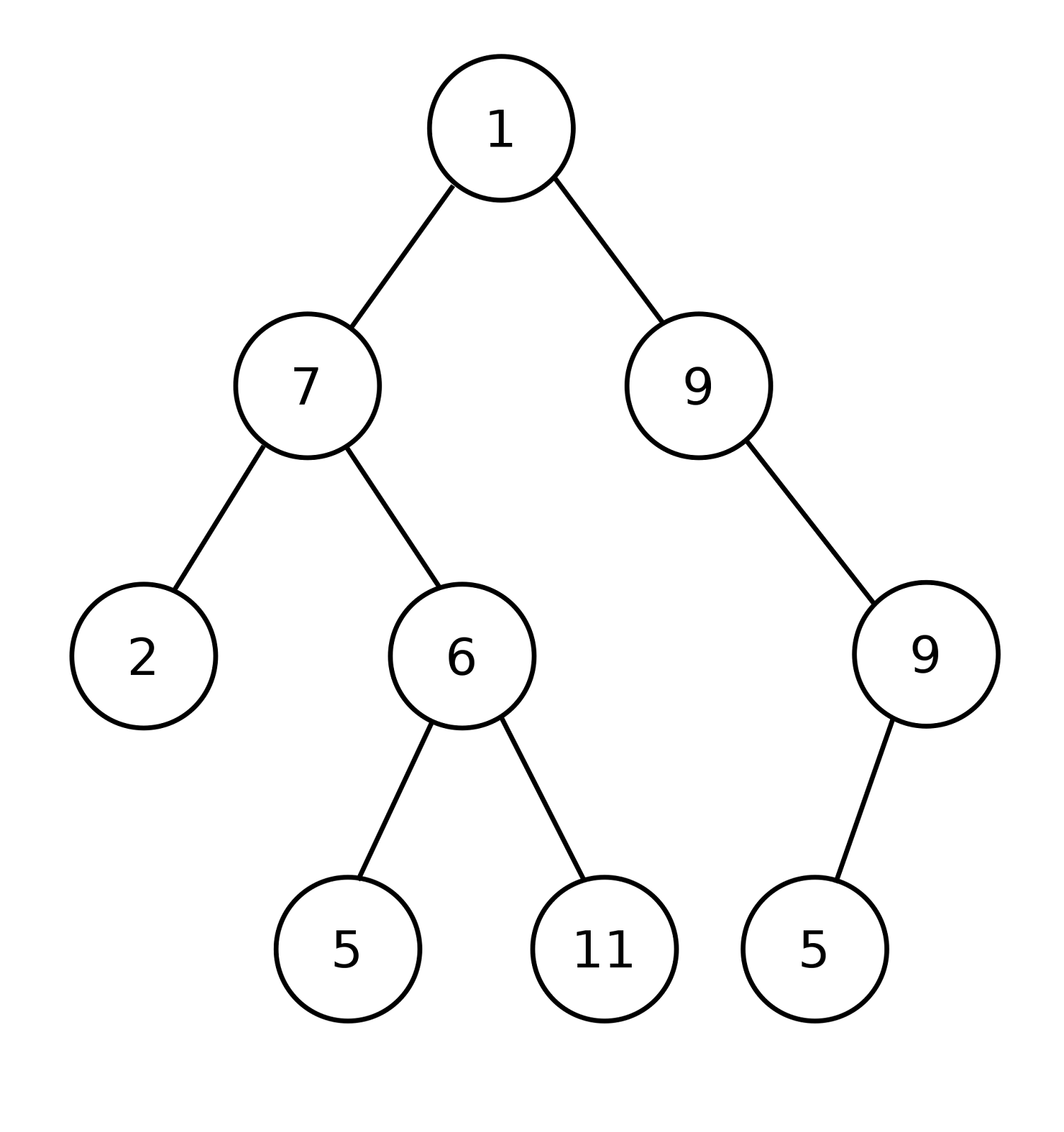
Yükseklik: Ağacın boyu hakkında bilgi veren, kök düğümden en uzaktaki yaprak düğüme kadar olan mesafeyi belirten kavramdır. Yandaki ağacın yüksekliği 4’tür.
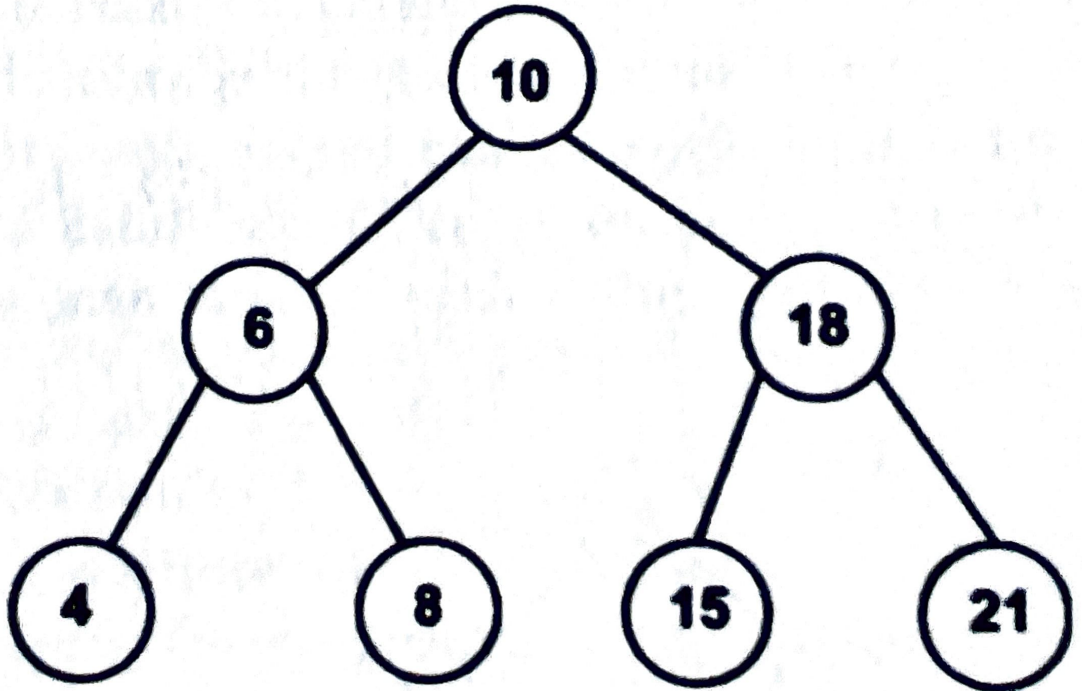
Dolu Ağaç: Her düğümü iki oğula sahip olan ya da hiç oğulu olmayan (yaprak) düğümlerden oluşan ağaç yapısı doludur.
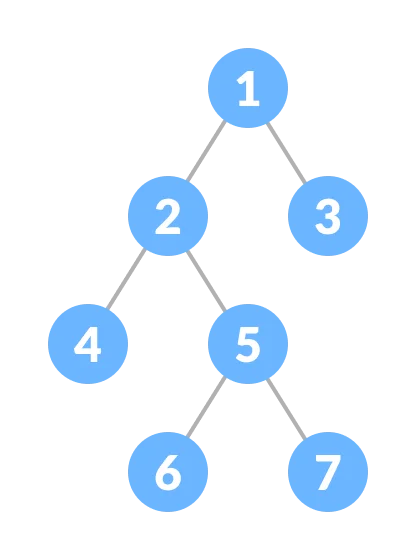
Tam Ağaç: Tabandakiler hariç, her düğümün iki oğulu olan ağaçtır. Yapraklar sola dayalı olmalıdır. Son düğümün sağ yaprağı olmak zorunda değildir. Yandaki ağaç hem dolu hem tam bir ağaçtır.
Alıştırmalar
8 (kökün) derinliği kaçtır?
5 ile 4’ün derinliği?
2’nin derinliği?
Ağacın yüksekliği kaçtır?
Dolu ağaç mıdır?
Tam ağaç mıdır?
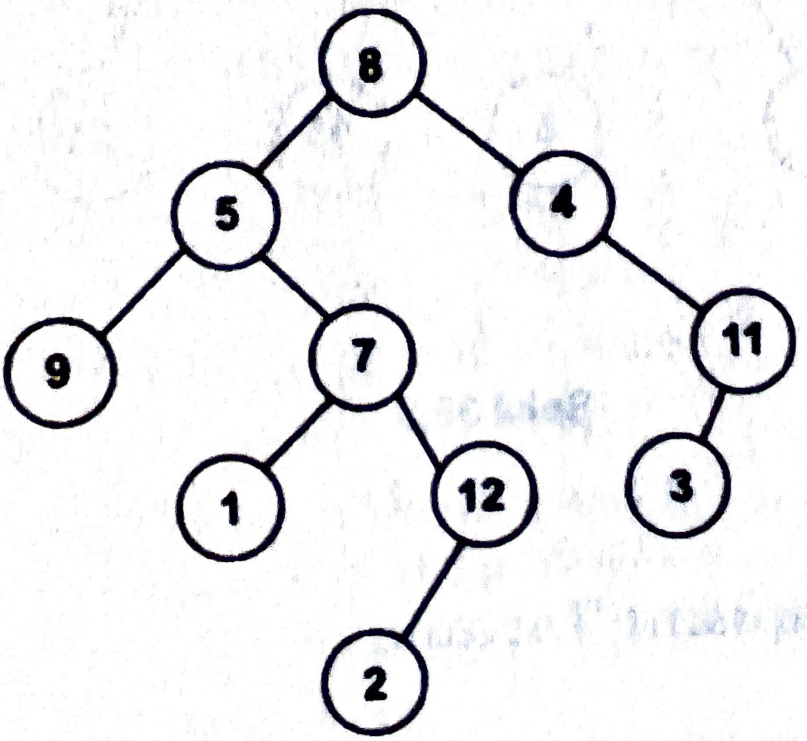
Aşağıda ağaçla ilgili verilen bilgilerden hangisi veya hangileri yanlıştır?
Ağaçlar hiyerarşik ilişkileri göstermek için kullanılır.
Her ağaç düğümler (node) ve kenarlardan (edge) oluşur.
Her bir düğüm bir nesneyi gösterir.
Her bir kenar (bağlantı) iki düğüm (node) arasındaki bağlantıyı gösterir.
Arama işlemi, bağlı listelere göre çok yavaş yapılır.
ÖZET
Doğrusal olmayan hiyerarşik bir veri yapısıdır.
Düğümlerden ve kenarlardan oluşur.
Her bir kenar iki düğüm arasındaki bağlantıyı gösterir.
Arama işlemi, bağlı listelere göre daha hızlıdır.
Çalışma Sorusu
Örnek bir ikili ağaç kodunu C ile yapay zekaya yazdırıp:
